亚洲日本免费-啊轻点灬太粗太长了三男一女-麻豆av电影在线观看-日韩一级片毛片|www.grbbt.com

生成隨機(jī)數(shù)看似容易，但其難度卻出乎意料——尤其是在隨機(jī)數(shù)的概率分布非常復(fù)雜的情況下。

在科學(xué)研究中（例如在訓(xùn)練神經(jīng)網(wǎng)絡(luò)時(shí)），經(jīng)常會(huì)遇到這種情況。在這種情況下，研究人員可以使用一種通用計(jì)算最早使用的技術(shù)：Metropolis算法。該算法于1953年首次在開創(chuàng)性的MANIAC計(jì)算機(jī)上運(yùn)行，而它的現(xiàn)代版名稱則是馬爾科夫鏈蒙特卡羅（MCMC）算法。

7月12日，來自IBM Quantum的科學(xué)家Layden等人在《自然》雜志上撰文，通過使用量子計(jì)算機(jī)來加速程序的性能，報(bào)告了這一算法發(fā)展中更為現(xiàn)代的轉(zhuǎn)折。

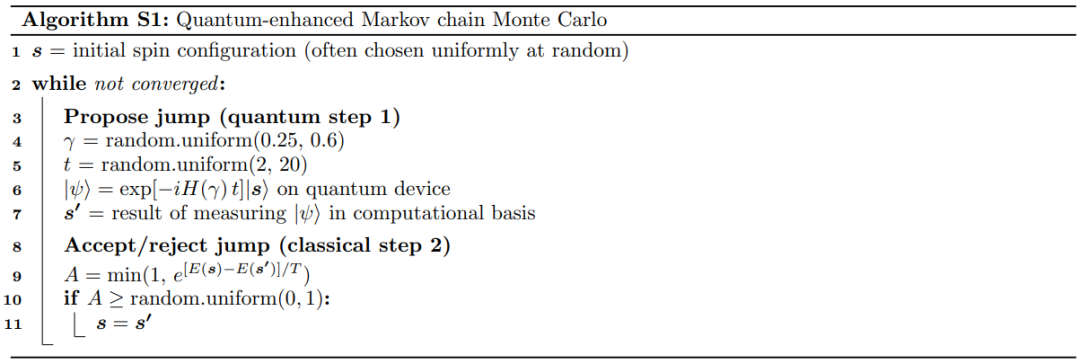
“Quantum-enhanced Markov chain Monte Carlo”

MCMC算法是一種根據(jù)指定概率分布生成隨機(jī)數(shù)的框架，這項(xiàng)任務(wù)被稱為采樣。該框架包含多種變體，所有變體都涉及樣本的迭代；經(jīng)過足夠多的循環(huán)后，需要保證樣本的分布符合所需的目標(biāo)分布。

這一過程中的每次迭代都包含兩個(gè)部分：

– 建議步驟，即在當(dāng)前樣本的基礎(chǔ)上建議一個(gè)樣本；

– 接受或拒絕步驟，即接受新樣本作為迭代中的下一個(gè)樣本，或拒絕新樣本以重復(fù)上述過程。

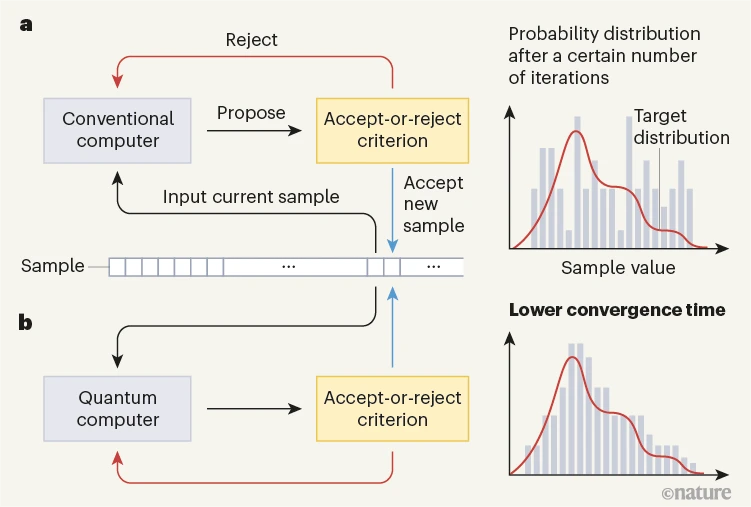
馬爾科夫鏈蒙特卡羅（MCMC）算法從目標(biāo)概率分布中抽取隨機(jī)數(shù)，涉及的兩個(gè)步驟：提出一個(gè)樣本，然后接受該樣本作為迭代中的下一個(gè)樣本；或者拒絕該樣本，從而觸發(fā)該過程重新開始。這兩個(gè)步驟的設(shè)計(jì)都必須保證足夠的迭代次數(shù)，以便最終得到符合目標(biāo)分布的樣本，實(shí)現(xiàn)這一目標(biāo)所需的迭代次數(shù)稱為收斂時(shí)間(convergence time)。具體來說，樣本收斂到目標(biāo)分布的迭代次數(shù)比使用傳統(tǒng)MCMC算法的迭代次數(shù)更少。

MCMC 算法的變體可通過每個(gè)步驟所使用的不同策略來區(qū)分。最重要的是，這兩個(gè)步驟必須以這樣一種方式構(gòu)建，即保證重復(fù)這兩個(gè)步驟最終得到的樣本分布符合所需的分布。因此，“需要多長時(shí)間”是任何MCMC變體的關(guān)鍵屬性。

在樣本按照目標(biāo)分布分布之前，這個(gè)過程需要重復(fù)1000次嗎？還是一百萬次？

所需的迭代次數(shù)稱為收斂時(shí)間，它取決于隨機(jī)變量的維度——描述采樣變量所需的比特?cái)?shù)。維數(shù)越大，收斂時(shí)間越長。不幸的是，對(duì)于目前使用的大多數(shù) MCMC 變體而言，收斂時(shí)間與變量維度的確切數(shù)學(xué)關(guān)系并不嚴(yán)格。然而，這并沒有阻止人們使用MCMC算法：他們傾向于利用收斂的經(jīng)驗(yàn)和統(tǒng)計(jì)特征。

Layden等人設(shè)計(jì)了一種MCMC變體：利用量子計(jì)算機(jī)在提議步驟中產(chǎn)生樣本。在任何迭代中，隨機(jī)樣本都被編碼為量子態(tài)，并對(duì)其進(jìn)行一系列量子運(yùn)算以產(chǎn)生輸出態(tài)，該輸出態(tài)可被測量以生成新樣本。這本身并不特別：在MCMC算法的提議步驟中，幾乎任何程序都可以用來生成新樣本（包括簡單地對(duì)當(dāng)前樣本施加噪聲）。

然而，此次的研究人員必須能夠證明這些步驟收斂到了目標(biāo)分布，而這對(duì)于任意的提議程序來說是不可能的。這就引出了Layden及其同事的關(guān)鍵創(chuàng)新：他們?cè)O(shè)計(jì)了一套量子操作，當(dāng)量子提議步驟與標(biāo)準(zhǔn)的接受或拒絕步驟相結(jié)合時(shí)，就可以驗(yàn)證收斂性。

作者通過數(shù)值模擬和早期量子計(jì)算硬件實(shí)驗(yàn)相結(jié)合的方式，展示了他們的量子增強(qiáng)MCMC算法。他們的研究結(jié)果表明了迭代對(duì)目標(biāo)分布的預(yù)測收斂性。更重要的是，他們還證明了該收斂速度快于之前為提議步驟設(shè)計(jì)的幾種經(jīng)典替代方案。

實(shí)際的收斂速度很難測量，作者僅對(duì)有限復(fù)雜度的過程進(jìn)行了測量——那些目標(biāo)變量分布最多可由10比特描述的過程；他們還對(duì)20比特變量目標(biāo)分布的收斂率進(jìn)行了近似計(jì)算。

在所有情況下，他們都發(fā)現(xiàn)了令人信服的證據(jù)，證明量子版MCMC算法的收斂速度比經(jīng)典版更快。他們根據(jù)經(jīng)驗(yàn)確定，這種速度提升是多項(xiàng)式的，量子增強(qiáng)策略的收斂時(shí)間約為傳統(tǒng)策略收斂時(shí)間的立方根。

這種速度提升從何而來？與大多數(shù)量子增強(qiáng)一樣，很難將其歸因于量子系統(tǒng)的任何一個(gè)特征。Layden等人提供的數(shù)字證據(jù)表明，他們所選擇的量子操作在生成多樣化提案與滿足目標(biāo)概率分布所施加的約束之間取得了微妙的平衡：這是經(jīng)典提案策略難以實(shí)現(xiàn)的權(quán)衡。

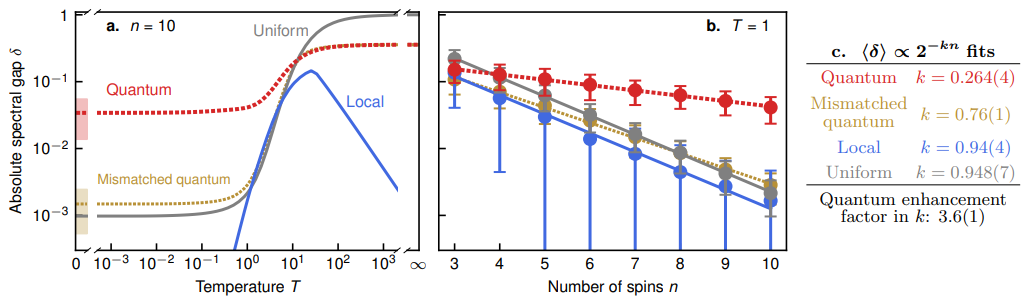
平均收斂速率模擬。

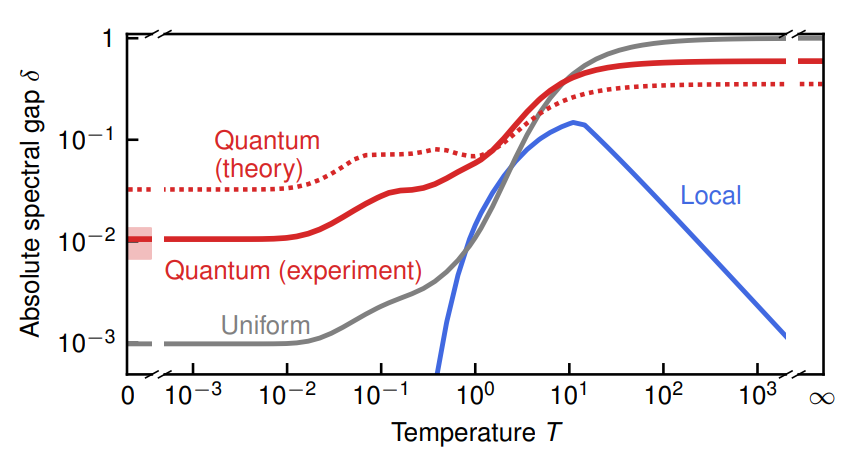
收斂率實(shí)驗(yàn)。

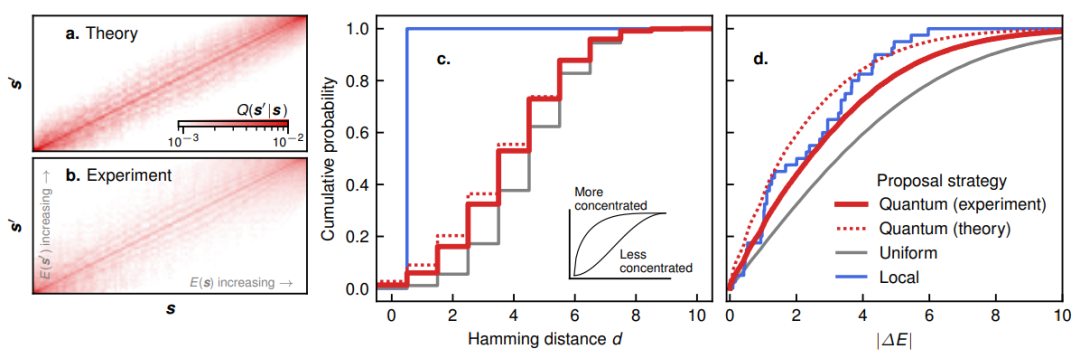
量子加速機(jī)制。

盡管Layden及其同事的工作很全面，但也存在一些局限性。

首先，量子增強(qiáng)算法的收斂性證明只有在量子操作完美執(zhí)行的情況下才是有效的：在硬件不產(chǎn)生任何噪聲的情況下。然而，他們的實(shí)驗(yàn)結(jié)果表明，收斂率對(duì)噪聲具有一定的穩(wěn)健性，尤其是當(dāng)硬件噪聲可以隨機(jī)化時(shí)。

其次，加速收斂僅在小規(guī)模問題中觀察到，在更大規(guī)模問題中可能會(huì)消失，特別是在存在噪聲的情況下。如果作者對(duì)加速原因的解釋是正確的，并且如果硬件噪聲可以在更大尺度上被抑制，加速很可能會(huì)持續(xù)下去——但這在現(xiàn)階段還遠(yuǎn)遠(yuǎn)不能確定。

最后，盡管Layden等人已經(jīng)證明他們的量子增強(qiáng)算法比一些常見的經(jīng)典提議策略收斂更快，但他們還沒有測試更多MCMC變體。因此，這一差距有可能被現(xiàn)有的或可能設(shè)計(jì)出的其他經(jīng)典提議策略彌補(bǔ)，甚至有可能是受到這項(xiàng)工作的啟發(fā)。

盡管存在這些局限性，Layden及其同事的研究為早期含噪聲量子計(jì)算機(jī)生成有用的解決方案提供了一個(gè)重要而令人興奮的應(yīng)用，同時(shí)也為富有成果的未來研究確定了許多方向。

參考鏈接：

[1]https://www.nature.com/articles/s41586-023-06095-4

[2]https://www.nature.com/articles/d41586-023-02176-6

來源：光子盒